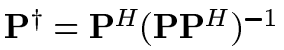Deep Learning For Channel Estimation In OFDM (Orthogonal Frequency-Division Multiplexing) Systems
As mentioned in the NQI post, data is extremely important for HFC networks. In this post, we will be taking a look at a very interesting paper published in one of the top high impact journals in CS, the IEEE Wireless Communications Journal. This article shows that it is indeed becoming increasingly important to use the data that is available, since publicly available Machine Learning methods can be applied to it with huge success.
First, a few notes on the theoretical background. The method that was applied here belongs to Deep Learning, which is a part of the larger set of Machine Learning methods, which in turn is a part of Artificial Intelligence. Obviously, this is a very hyped up field currently, so it's not surprising at all that the Telecommunications field is starting to feel the effectiveness of Machine Learning.
Now, there are many methods in Machine Learning, ranging from simple linear regression over decision trees to clustering methods such as k-means. Neural networks are also part of Machine Learning. These are extremely versatile structures that are parameterized by their architecture (number of nodes and number of layers) and the optimizer. If you're curious, here is a related post that dives deeper into Machine Learning. Deep Learning is a subset of Machine Learning and uses neural networks with multiple layers.
The paper in question (Ye et al.) applies a deep neural network to channel estimation and compares it with ordinary methods that are well-known in the field. One such popular method is using pilot signals and a least squares estimator to find the channel matrix.
Pilot signals are used for channel estimation - following Biguesh et al., over time, a set of training signals (or pilot signals) are sent and corresponding responses collected. Using the least squares estimation (also popular in linear regression), the channel matrix is estimated from the training samples and the responses:
with S being the received signals, H being the channel matrix, P the training signals and V the noise vector. The linear squares estimator for H is defined as:
with
and x to the power of H being the Hermitian transpose of x. A least squares estimator can often be solved in closed form (as shown here), but sometimes the inverse of the right matrix does not exist. In that case, an iterative solver is needed, such as gradient descent.
It is of course more efficient when less pilot signals are needed, since less time and resources are spent for the estimation. This is where the Deep Learning approach comes in. The paper shows a very interesting result: Compared to other methods, Deep Learning is more robust and needs less pilot signals to achieve a similar performance.
Another interesting result is related to the cyclic prefix. The cyclic prefix is used in OFDM systems to mitigate symbol interference. Again, the Deep Learning model shows very good robustness when omitting the cyclic prefix (which leads to less time spent).
The Figure below illustrates both results (BER is the bit error rate, which we want to be as low as possible):
It is interesting to note that the model architecture is rather large: They use three hidden layers of sizes 500, 250 and 120, with 256 being the input size and 16 the output size. Since they are fully connected, this gives us a ball park estimate of 61.4B parameters (!) that need to be trained. Thus, it is not clear how this would scale.
Deploying this method and testing it on large systems is something that takes time, but still: This suggests that OFDM systems could soon be seeing Deep Learning as their main method for channel estimation. It will be very interesting to see whether this happens, as it was not clear how large the dataset in Ye et al. was and how well it would scale to a real system with millions of CPEs.
References:
Biguesh et al., Training-Based MIMO Channel Estimation: A Study of Estimator Tradeoffs and Optimal Training Signals
Ye et al., Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems
* Figure directly from Ye et al.